Forces and Motion: Dynamics

Forces and Motion: Dynamics

Chapters for this unit are 1, 2, & 3

1. Velocity and acceleration in one and two dimensions
2. Forces and Newton's Laws (Vectors)
3. Universal Law of Gravity
4. Circular motion and forces that result in circular motion

Kinematics

This section is pretty much a review of grade 11 with some additions. Terms that you should be familiar with

Here's a sample question that you should be able to do.

You must be able to work with these equations

Working with Vectors: Addition and Resolution

In Fig. 1 two vectors are being added using the head to tail method. You should also realize that Pythagorean theorem could have been used, follwed by sinΘ = O/H and inverse to obtain the angle or direction of the vector.
In Fig. 2 vector resolution is used to break the given vector into its two components on the x, y or horizontal, vertical axis. Using laws of sines and cosines will allow you to calculate the x and y component of the vector.

Note: an accurately draw diagram will also eneable you to solve for the required vectors simply by measuring the magnitude (ruler) and angle of direction (protractor).
Can't Remember how to add or subtract vectors, then take a look at a Vector Arithmetic Java Applet

Projectile motion incorporates much of the above concepts into one problem. A "making connections" problem. Vector resolution would be used to solve this type of problem.

Projectile Motion

Is the vertical velocity positive or negative as the object proceeds upward? It will depend upon how you set up the vectors. See Fig 2

Example: A bowman shoots an arrow into the air. What are the possible situations that arise:

1. The arrow goes straight up and then back down again. No horizontal motion.
2. The arrow is shot at some angle to the horizontal. I now has both vertical and horizontal motion.
3. Is the motion, vertical or horizontal experencing an applied force? If so acceleration will occur.
4. The arrow has a initial velocity. Remember that velocity is a vector an as such has a direction attached to it and must be dealt with in the problem.
5. Where is the (0,0) point on your accurate diagram or graph?
6. Will you solve this problem geometricly or algebraicly? Can you work with the Laws of sines and cosines?
7. In order for the arrow to move an applied force must be exerted. Force is a vector in the same direction as the acceleration and velocity unless other forces are applied.
8. The force of gravity will dictate the overall motion of the arrow.
9. Is the wind blowing? this leads to more complications.
10. Where is the bowman standing? On the ground? On top of a cliff?
11. How high above the ground is the bowman before the arrow is shot?
12. Time can be worked into the problem. How long is the arrow in the air?
13. Is the bowman standing still or is he moving? If he is moving then this velocity must be encororated into the problem.
14. Is air resistance to be considered?

Projectile Motion Equations

1. d_y = height =
2. d_x = range =
3. t_r = rise time = t_f = fall time =
4. flight time, t =

Take a crack at Projectile Motion by trying to Hitting the Target  

Frames of Reference

When you start pulling the wagon, you notice that the ball ends up in the back of the wagon. Why? There are (at least) two possible lines of reasoning:

1. Viewed from beside the wagon: The ball was at rest in the wagon. The ball has inertia, so when the wagon began to accelerate (because you were pulling it), the ball "wants" to stay at rest. The ball ends up in the back of the wagon because the wagon accelerated, and the ball stayed were it was.
2. Viewed from inside the wagon (or moving with the wagon): The ball suddenly started rolling toward the back of the wagon. What pushed it? I don't know - "g forces", maybe. What exerted this mysterious "g force" on the ball? I don't know, maybe the acceleration of the wagon exerted the "g force".

In the second case, life is not so simple. Here, the ball no longer obeys Newton's First Law - it suddenly jumps up and takes off toward the back of the wagon all by itself! No, wait a minute - that can't happen. There has to be some force that pushed the ball - but where did this force come from? You didn't see anything pushing the ball - but something has to be pushing, Oh my! What a mess!
One of the points of this "thought experiment" is that all reference frames are not created equal. In dynamics, some reference frames are clearly easier to use than others, and you need to know the difference. In the first case, your frame of reference is the Earth, which is not accelerating (Ok, see below...). In this frame of reference Newton's First Law works simply and wonderfully. A reference frame that is not accelerating is called an inertial reference frame - because the Law of Inertia works there.
On the other hand, when you were moving with the wagon, you were viewing the motion from an accelerating reference frame (often called a non-inertial reference frame). In this reference frame, Newton's First Law does not seem to work, since the ball seems to "take off" toward the back of the wagon all by itself. Since people seem to have a deeply-ingrained belief that balls don't "just take off by themselves", they tend to believe that there must be a force acting on the ball to cause this behavior - the "g force". This, however, leads to even more problems and muddled thinking - what exerts this mysterious "g force"?
The easy answer is - There is no force! Certainly, no force was necessary to explain the (same) motion in situation 1 - and a force is either there, or it isn't. You can't have a force when you look at a situation in one way, and no force when you look at the same situation in another way! This "g force" is an example of a fictitious force - there is actually no force! Fictitious forces tend to appear when you are viewing a motion from an accelerating reference frame.

An additional note of Frames of Reference

Dynamics: Forces in Action

• F_m = any applied force which may or may not cause the object to move
• F_g = is the force of gravity downward equal to the mass x 9.83 m/s²
• F_n = is called the normal force, it is what hold the object up or on the surface. It is the reaction force to F_g and is always perpendicular to the surface.
• F_f = is the force of friction acting between the object ant the surface it is on and is always a reaction force to F_m.
  F_f may or may not be equal to F_m but can never be less than F_m. Why?

Contact Forces and a free body diagram
Here is an example...

1. Normal Force Note  
2. Tension Note  
3. Static Friction Note  
4. Kinetic Friction Note  

Friction on an Inclined Plane

Forces acting on an object on an inclined plane are shown in Fig 3. Identification of forces as follows: F_g : is the force of gravity acting on the object; the object's weight, units are in Newtons (N)
F_n : is the normal force perpendicular to the surface of the inclined plane; has a magnitude of cos F_g
F_f : is the force of friction opposite to the motion of the object
F_m: is the resultant force causing the motion of the object parallel to the inclined plane and is caused by gravity; has the magnitude of sin F_g
Angle θ : is the angle of the inclined plane
The net force of motion on the object is the sum of F_m + F_f. Remember that these two forces act in opposite directions and numerically are subtracted. The overall or net force is NOT shown in Fig 3 because it depends upon the magnitude of the other forces.

Friction occurs when a body slides across a surface and is a reactionary force, that is, it opposes the applied force and acts in the opposite direction of the motion. Three situations do arise and are list below:
When F_f is greater than F_m the object is at rest. The force of friction is great enough to prevent the object from sliding down the plane. When F_f equals F_m the object is just of the verge of moving. In this situation F_m is called the limiting static friction (page 97 text book). When F_f is less than F_m the object is moving down the inclined plane and the force F_f that opposes this motion is called kinetic friction. On an inclined plane gravity is the force that causes the object to move (unless there is an external applied force). Because of the angular inclination of the plane resolution of forces can be applied to F_g. On resolution, some of F_g will be equivalent to F_n and the rest will become F_m, the force of motion. Projecting F_g onto the F_n line (see diagram Fig 3.), F_n has a value of cos F_g and F_m has a value of sin F_g. As you can see the smaller the value of the greater the value of F_n and the less value of F_m. The greater the angle the greater F_m and the greater the probability that the object will slide down the ramp.

Coefficient of Friction

Uniform Circular Motion

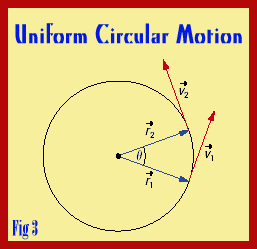
Uniform circular motion is actually a specific type of motion. An object is undergoing uniform circular motion if it is traveling at a constant speed while moving in a circle. For example, if you drive a car around a circle while maintaining a constant speed, you are performing uniform circular motion.
The main requirements for uniform circular motion are

1. a constant speed
2. motion in a circle.

Velocity also includes a direction in addition to the speed. This makes all the difference in the world. While an object undergoing uniform circular motion is moving at a constant speed, it is not moving at a constant velocity. This is because the direction of its motion continues to change as it moves around the circle. And, because the direction is always changing, its velocity is not constant.
Remember, a constant velocity only occurs if both the object's speed and its direction are constant. The only way this can occur is if the object is moving in a straight line and at a constant speed.

In the picture below, the blue dot is moving at a constant speed around a circle. In other words, the blue dot is undergoing uniform circular motion. Notice that while the speed is constant, the direction continues to change as the blue dot moves around the circle. In the figure below, the direction of the velocity (at any given point on the circle) is denoted by the red arrow.

Newton's 1st Law of Motion tells us that, whenever an object's velocity is changing, there must be some external net force acting on the object to cause this change in velocity. Another way to think about this is to think of acceleration. Since the velocity of an object undergoing uniform circular motion is changing, it must be accelerating. This is because acceleration is defined as the change in velocity over time. Therefore, whenever an object's velocity is changing, it is experiencing an acceleration. According to Newton's 2nd Law of Motion, this acceleration must be caused by some external net force, once again, leading to the conclusion that an object undergoing uniform circular motion must be experiencing an external net force.

Putting all these points together, we find that

1. an object undergoing uniform circular motion has a velocity that is not constant. The velocity is not constant (even though the speed is constant) because the direction of the velocity continues to change as the object moves around the circle.
2. Because the object's velocity is changing, we know the object is experiencing an acceleration as it moves around the circle.
3. An object can only experience an acceleration when there is an external net force acting on the object because it is the external net force which causes an object to accelerate. In other words, when we see an object undergoing uniform circular motion, we know there must be some force acting on that object which is responsible for making the object move around a circle at a constant speed.

Main Conclusions

1. In general, if we want to increase the speed with which the object undergoes uniform circular motion (while keeping the radius unchanged), we need to increase the amount of force pulling inward on the object. Next, we showed how the above formula tells us exactly how much to change the amount of force in order to make the object's speed increase. In particular, the amount of force (required to make an object undergo uniform circular motion) is related to the object's speed by the factor below.

   F_c is related to the speed, v, by the following term: v²

2. In general, if the radius of the circle, around which the object undergoes uniform circular motion, is increased (while keeping the object's speed unchanged), the amount of force required to make the object undergo uniform circular motion (around the new circle with the larger radius) is decreased. Next, we showed how the above formula tells us exactly how much the amount of force changes as the radius of the circle changes. In particular, the amount of force (required to make an object undergo uniform circular motion) is related to the radius of the circle by the factor below. F_c is related to the radius of the circle by the following factor: 1/r

If an object is travelling in a circular path at constant speed its velocity is changing because, even though the magnitude of the velocity remains constant, the direction of the velocity is changing continuously.
The velocity vector points along a tangent to the circle, in the direction that the object would tend to move if it were suddenly released.
The acceleration acts in the same direction as the change in velocity.
The acceleration is called centripetal acceleration. It always acts inward, toward the centre of the circle, in the same direction as the change in velocity, perpendicular to the velocity vector.
The magnitude of the centripetal acceleration is given by:



where R is the radius of the circle, T is the period of revolution, f is the frequency of revolution, and ac is the magnitude of the centripetal acceleration.
The subscript c serves as a reminder of the vector nature of the acceleration. Its direction is constantly changing at every position along the circular path.

From Newton's Second Law: The force acts in the same direction as the acceleration. The force, directed towards the centre of the circle,
is called centripetal force.

For an extra look at Centripetal Forces

For a complete note on Circular Motion (See lessons 1 & 2)

Here's a summary from the Physics Classroom on Circular Motion.

*****************

Any object moving in a circle (or along a circular path) experiences a centripetal force; that is there must be some physical force pushing or pulling the object towards the center of the circle. This is the centripetal force requirement. The word "centripetal" is merely an adjective used to describe the direction of the force. We are not introducing a new type of force but rather describing the direction of the net force acting upon the object which moves in the circle. Whatever the object, if it moves in a circle, there is some force acting upon it to cause it to deviate from its straight-line path, accelerate inwards and move along a circular path. Three such examples of centripetal force are shown below.

******************

To summarize, an object in uniform circular motion experiences an inward net force. This inward force is sometimes referred to as a centripetal force, where "centripetal" describes its direction. Without this centripetal force, an object could never alter its direction. The fact that the centripetal force is directed perpendicular to the tangential velocity means that the force can alter the direction of the object's velocity vector without altering its magnitude.

**********************

Applying the concept of a centripetal force requirement, we know that the net force acting upon the object is directed inwards. Since the car is positioned on the left side of the circle, the net force is directed rightward. An analysis of the situation would reveal that there are three forces acting upon the object - the force of gravity (acting downwards), the normal force of the pavement (acting upwards), and the force of friction (acting inwards or rightwards). It is the friction force which supplies the centripetal force requirement for the car to move in a horizontal circle. Without friction, the car would turn its wheels but would not move in a circle (as is the case on an icy surface). This analysis leads to the free-body diagram shown at the right. Observe that each force is represented by a vector arrow which points in the specific direction which the force acts; also notice that each force is labeled according to type (Ffrict, Fnorm, and Fgrav). Such an analysis is the first step of any problem involving Newton's second law and a circular motion.

*******************

Sample Problem #1 A 900-kg car makes a 180-degree turn with a speed of 10.0 m/s. The radius of the circle through which the car is turning is 25.0 m. Determine the force of friction and the coefficient of friction acting upon the car.

Sample Problem #2 The coefficient of friction acting upon a 900-kg car is 0.850. The car is making a 180-degree turn around a curve with a radius of 35.0 m. Determine the maximum speed with which the car can make the turn.

For a solution to these two sample problems and scroll down to find the solutions

Gravitation and the Universal Law of Gravitation

Newton's Law of Universal Gravitation can be expressed as:

The weight of an object of mass m at the surface of the Earth is obtained by multiplying the mass m by the acceleration due to gravity, g, at the surface of the Earth. The acceleration due to gravity is approximately the product of the universal gravitational constant G and the mass of the Earth M, divided by the radius of the Earth, r, squared. (We assume the Earth to be spherical and neglect the radius of the object relative to the radius of the Earth in this discussion.) The measured gravitational acceleration at the Earth's surface is found to be about 983 cm/second/second.

More information of the The Value of G

Planetary and Satillite Motion: In Three Parts

1. Circular Motion Principles for Satellites
2. Mathematics of Satellite Motion
3. Energy Relations for Satellites

If you have questions ask them!