To the right we show two objects approaching each other at 60 km/hr relative to us. We shall assume that the two objects have equal masses and are constructed of a "sticky" material.

When they two objects collide they stick together. Since before the collision the two objects had equal masses and were moving in opposite directions at the same speeds, their inertia or momenta were equal and opposite. Thus after the collision they will be stationary relative to us. This is an example of the Principle of Inertia, also called Conservation of Momentum.

Now we imagine looking at the same collision for the reference frame of an observer moving to the left at 60 km/hr relative to the first one. The right hand (red) ball will be stationary for this person, but the left hand (blue) ball will be moving at 60 + 60 = 120 km/hr.

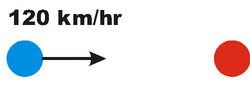
After the collision, the two balls stick together. Since the two balls that are stuck together have twice the mass of the left-hand (blue) ball by itself, after the collision the speed of the two must be one-half of 120 km/hr, i.e. 60 km/hr. Since for the first observer the two balls are stationary after the collision and the second observer is moving to the left at 60 km/hr, we can predict that after the collision the two balls will be moving at 60 km/hr relative to the second observer. So we have two ways of getting the result shown to the right: from Conservation of Momentum or from Galilean relativity.