Kinematics: In one dimension and with a constant acceleration:
Here's a list of all the formula you need. Only one version is listed.
If you wish to isolate for every variable in each formula feel free to do so. See example at the end of this note.
- vav represents the average velocity over the given time interval
- aav represents the average acceleration over the given time interval
- d or Δd represents the displacement traveled with the most common unit m. Note displacement and distance are most often the same unless stipulated.
- the Δ insinuates a change
- watch out for the squares in formula 6 & 7
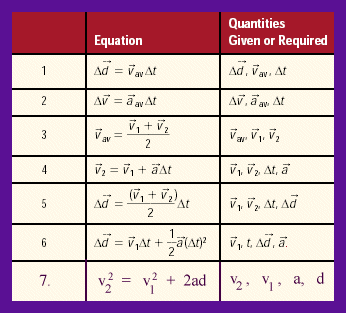
Caution: the most misused formula is #1, be careful with this one.
Kinematic Equations
For motion with constant acceleration and t0 = 0, we
can now derive a set of kinematic equations that will enable us to
solve all problems of this kind. These equations are:
- d = d0 +
v0 t + ½ a
t2
- v = v0 + a
t
- vav = (v +
v0)/2
- d = d0 +
vav t
- v2 =
v02 + 2 a (d -
d0)
Note: d -
d0 is the same as Δd or simply just d
You will notice there is no formula v = d/t written in these three lists. That should tell you something: don't use it, it probably won't work.
MORE
In this table you have FOUR versions of the same formula. The formula has been reworked to solve for a specific unknown.
| Solving for the velocity after the objects accelerates |
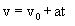 |
| Solving for the time |
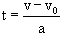 |
| Solving for the acceleration |
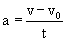 |
| Solving for the initial velocity |
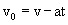 |
In these formulae
- vo represents the initial velocity and has an alternate designation of v1
(see below)
the most common units are m/s
- v represents the final velocity and has an alternate designation of v2
(see below)
the most common units are m/s
- a represents acceleration
its corresponding unit is m/s2
- t represents time
its corresponding unit is s
- see equation # 4 below

